Algorithm to Return All Combinations of k Elements from n

To generate all possible combinations of k elements from a given set of n elements, you can use a recursive algorithm. Combinations are distinct subsets of elements without regard to their order.

Understanding Combinations

What are Combinations?

Combinations are selections of elements from a set without considering the order of the elements. For example, given the set {1, 2, 3}, the combinations of 2 elements are {1, 2}, {1, 3}, and {2, 3}.

Implementing the Combinations Algorithm

Recursive Backtracking Algorithm for Combinations

To generate all combinations, you can use a recursive backtracking algorithm. The idea is to either include or exclude each element from the set in each recursive call, building all possible combinations along the way.

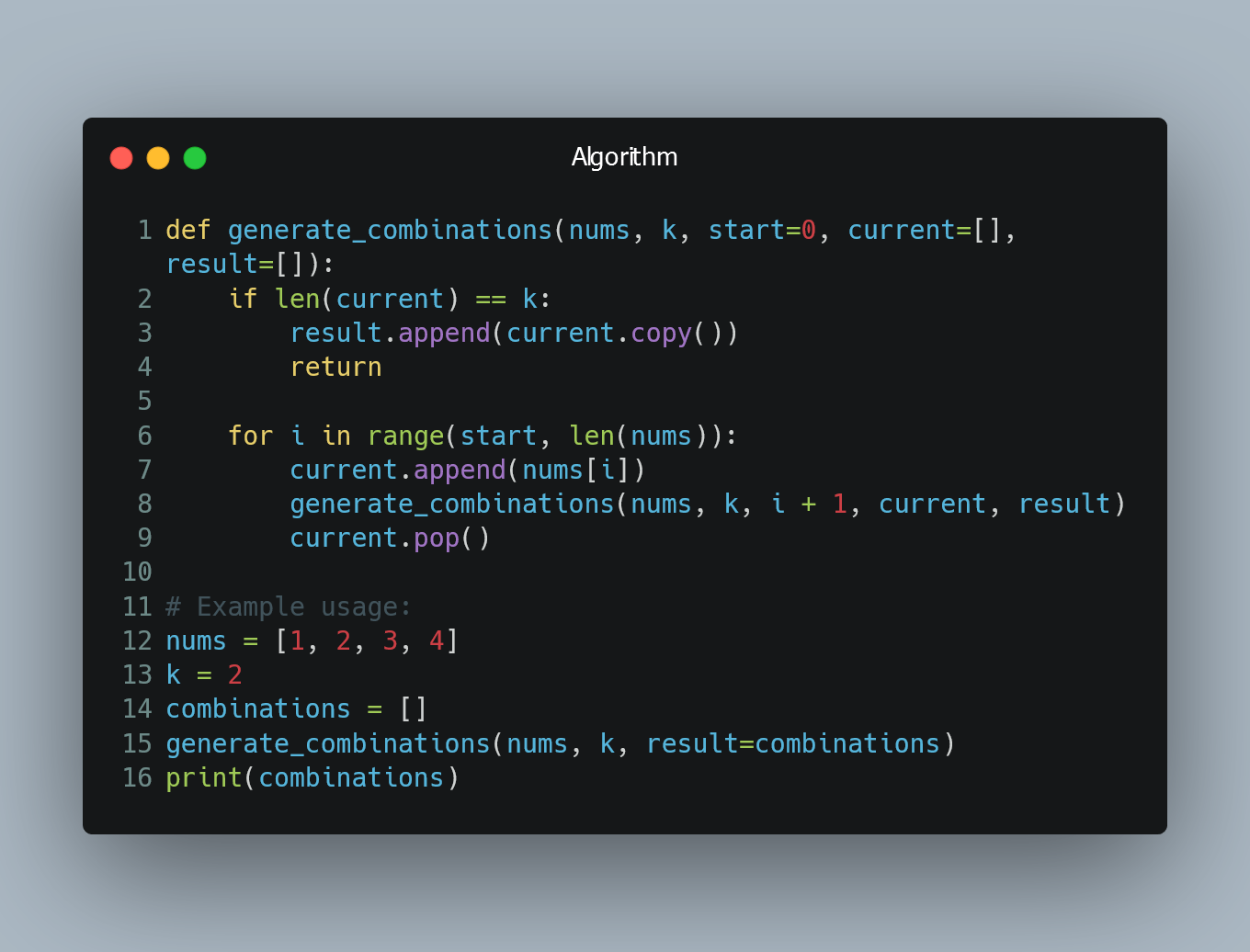
Example in Python

def generate_combinations(nums, k, start=0, current=[], result=[]):
    if len(current) == k:
        result.append(current.copy())
        return

    for i in range(start, len(nums)):
        current.append(nums[i])
        generate_combinations(nums, k, i + 1, current, result)
        current.pop()

# Example usage:
nums = [1, 2, 3, 4]
k = 2
combinations = []
generate_combinations(nums, k, result=combinations)
print(combinations)

Output

[[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

In this Python example, the generate_combinations function generates all combinations of k elements from the list nums. The function uses recursion and backtracking to explore all possible combinations and stores the results in the combinations list.