To generate all possible permutations of a list, you can use a common algorithm called "backtracking." This technique systematically explores all possible arrangements of the elements in the list, ensuring that each permutation is unique.
Understanding Backtracking
What is Backtracking?
Backtracking is a technique used to explore all possible solutions to a problem by incrementally building a solution and "backtracking" when a dead-end is reached. It's commonly used in combinatorial problems like generating permutations, combinations, and solving puzzles.
Implementing Permutations Generation
Backtracking Algorithm for Permutations
To generate all permutations of a list, you can use a recursive backtracking algorithm. The basic idea is to select elements one by one from the list and recursively generate the remaining permutations.
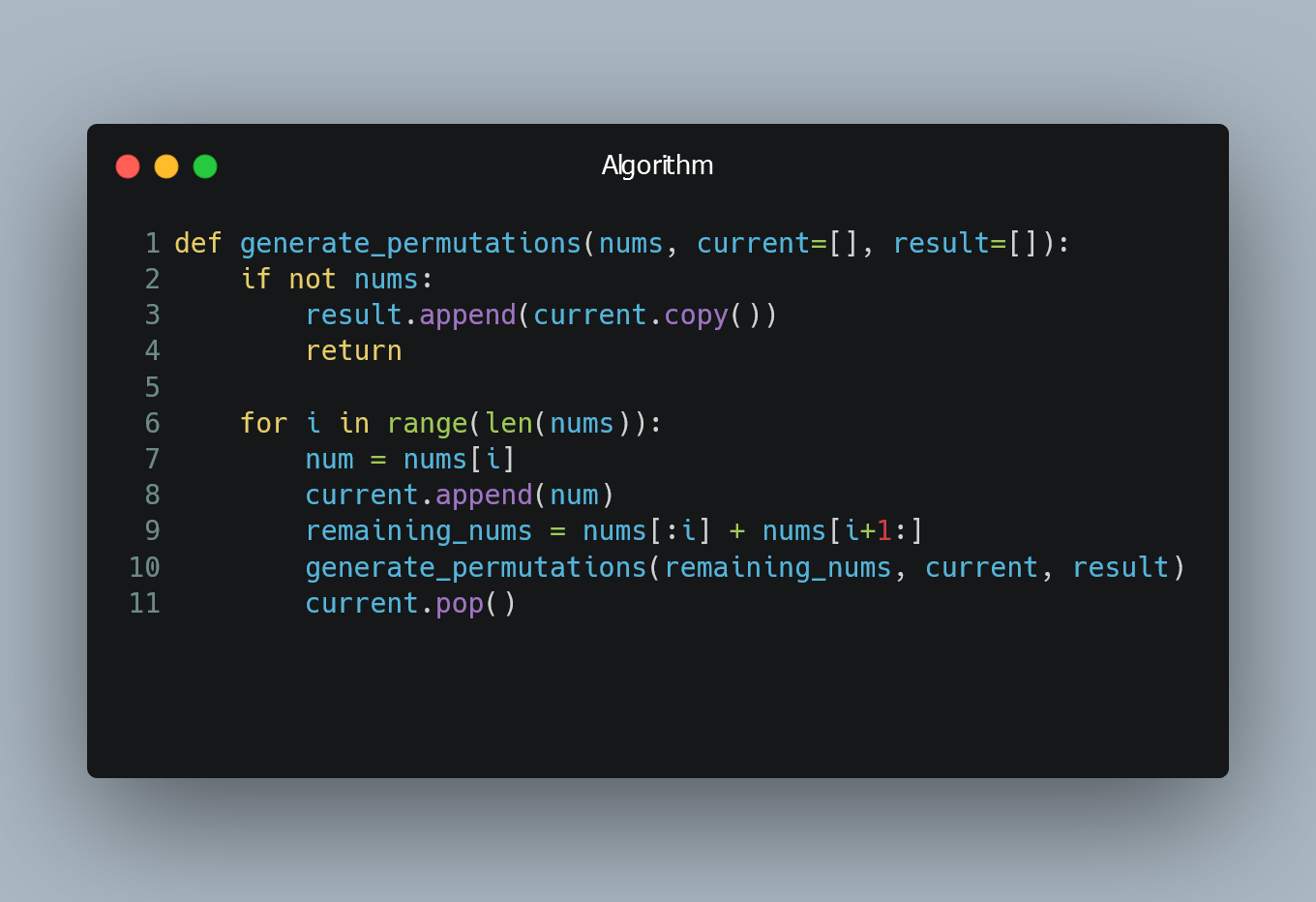
Example in Python
def generate_permutations(nums, current=[], result=[]):
if not nums:
result.append(current.copy())
return
for i in range(len(nums)):
num = nums[i]
current.append(num)
remaining_nums = nums[:i] + nums[i+1:]
generate_permutations(remaining_nums, current, result)
current.pop()
# Example usage:
nums = [1, 2, 3]
permutations = []
generate_permutations(nums, result=permutations)
print(permutations)
Output
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
In this Python example, the generate_permutations function generates all permutations of a list nums. The function uses recursion and backtracking to explore all possible combinations and store the permutations in the permutations list.
0 Comment

