When working with 32-bit integers, you may encounter scenarios where you need to count the number of set bits, i.e., the number of 1s, in the binary representation of the integer. This operation is also known as population count or Hamming weight.
Using Bit Manipulation
What is Bit Manipulation?
Bit manipulation involves performing operations at the individual bit level of an integer. By using bitwise operators, you can extract, modify, or analyze specific bits of an integer.
Counting Set Bits with Brian Kernighan's Algorithm
Brian Kernighan's algorithm is an efficient method to count the set bits in an integer. It relies on the fact that repeatedly performing n & (n-1) will turn off the rightmost set bit of the integer. By repeatedly applying this operation until the integer becomes zero, you can count the number of set bits.
Example in C++
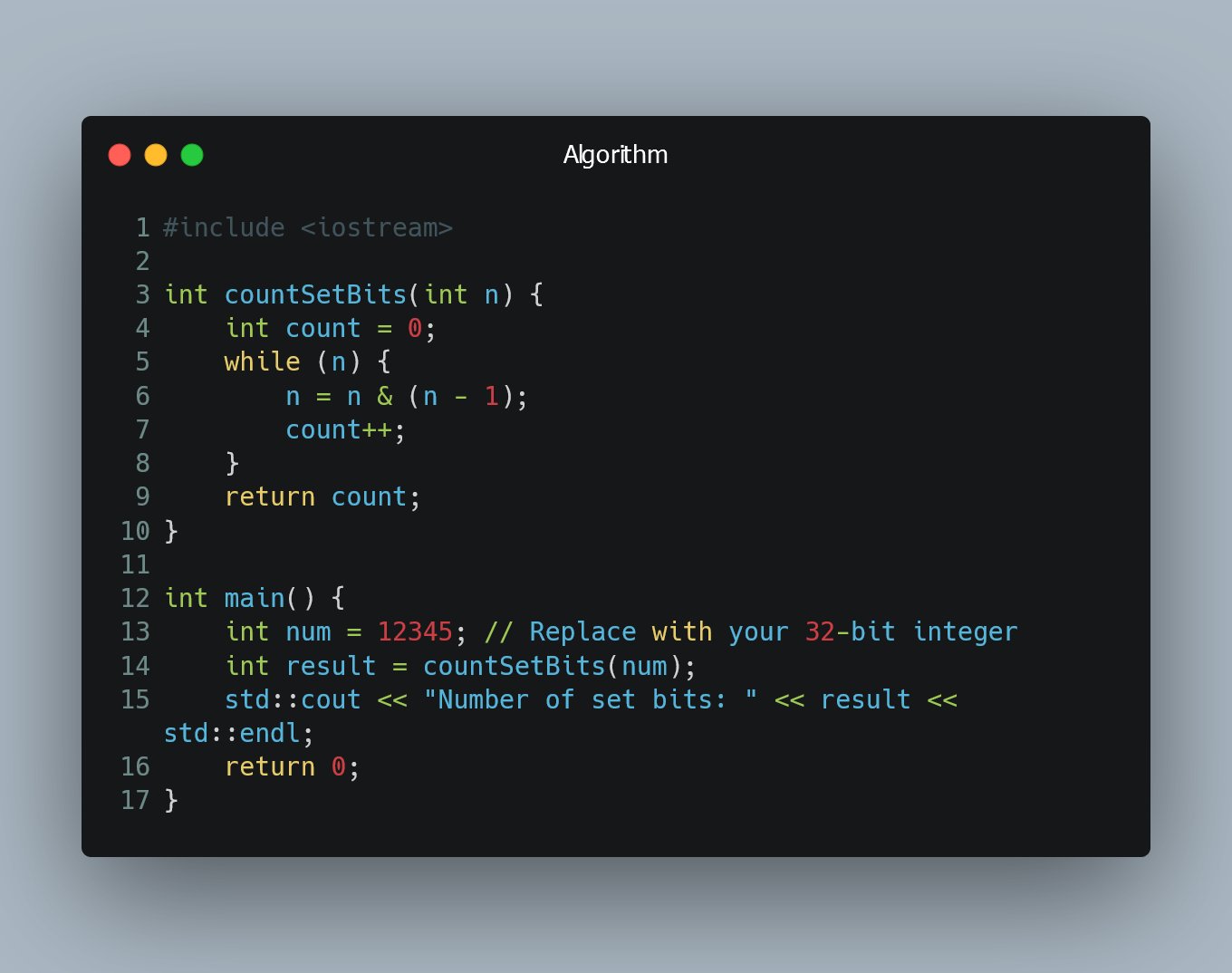
#include <iostream>
int countSetBits(int n) {
int count = 0;
while (n) {
n = n & (n - 1);
count++;
}
return count;
}
int main() {
int num = 12345; // Replace with your 32-bit integer
int result = countSetBits(num);
std::cout << "Number of set bits: " << result << std::endl;
return 0;
}
Example in Python
def count_set_bits(n):
count = 0
while n:
n = n & (n - 1)
count += 1
return count
num = 12345 # Replace with your 32-bit integer
result = count_set_bits(num)
print("Number of set bits:", result)
In both examples, the countSetBits function (C++) and count_set_bits function (Python) implement Brian Kernighan's algorithm to count the set bits in a 32-bit integer. The result is the number of 1s in the binary representation of the integer.
0 Comment

